Cauchy Trait Simulation

Source: R/rTraitCauchy.R

Simulate a continuous trait using the Cauchy Process

rTraitCauchy(
  n = 1,
  phy,
  model = c("cauchy", "lambda", "kappa", "delta"),
  parameters = NULL
)

Arguments

n

number of independent replicates

phy

a phylogeny in ape phylo format.

model

a phylogenetic model. Default is "cauchy", for the Cauchy process. Alternative are "lambda", "kappa", and "delta".

parameters

list of parameters for the model (see Details).

Value

If n=1, a numeric vector with names from the tip labels in the tree. For more than 1 replicate, a matrix with the tip labels as row names, and one column per replicate.

Details

The default choice of parameters is as follow:

model = cauchy

root.value = 0, disp = 1

model = lambda

root.value = 0, disp = 1, lambda = 1

model = kappa

root.value = 0, disp = 1, kappa = 1

model = delta

root.value = 0, disp = 1, delta = 1

See also

rTrait, rTraitCont

Examples

set.seed(1289)
phy <- ape::rphylo(40, 0.01, 0)
# One trait
y <- rTraitCauchy(n = 1, phy = phy, model = "cauchy",
                  parameters = list(root.value = 0, disp = 0.1))
y
#>          t1          t2          t3          t4          t5          t6 
#> -19.7836864  -6.4565183  -0.6540311 158.0987207 127.5360462 -89.8160998 
#>          t7          t8          t9         t10         t11         t12 
#>  -6.9966910 131.9668304   3.2243344 -36.8263533 -11.2891239  26.4793554 
#>         t13         t14         t15         t16         t17         t18 
#>  77.5240345 108.9499536 -18.4919200 132.4769952  -2.9577254 -17.9076511 
#>         t19         t20         t21         t22         t23         t24 
#> -15.0047732 -10.4484145  -1.7023756  16.5862768  -9.2665804  18.3067747 
#>         t25         t26         t27         t28         t29         t30 
#>  -9.9573878  -5.0490531 -35.9429867 131.0540121 -23.8539793  16.9864284 
#>         t31         t32         t33         t34         t35         t36 
#> -11.2525015 -14.5805471 -15.7367069 -92.1090761  -4.3144022  -9.0875610 
#>         t37         t38         t39         t40 
#> -17.2918197 -13.2481063 -39.8714221 -91.5614637 
plot(phy, x.lim = c(0, 750))
phydataplot(y, phy, offset = 150)

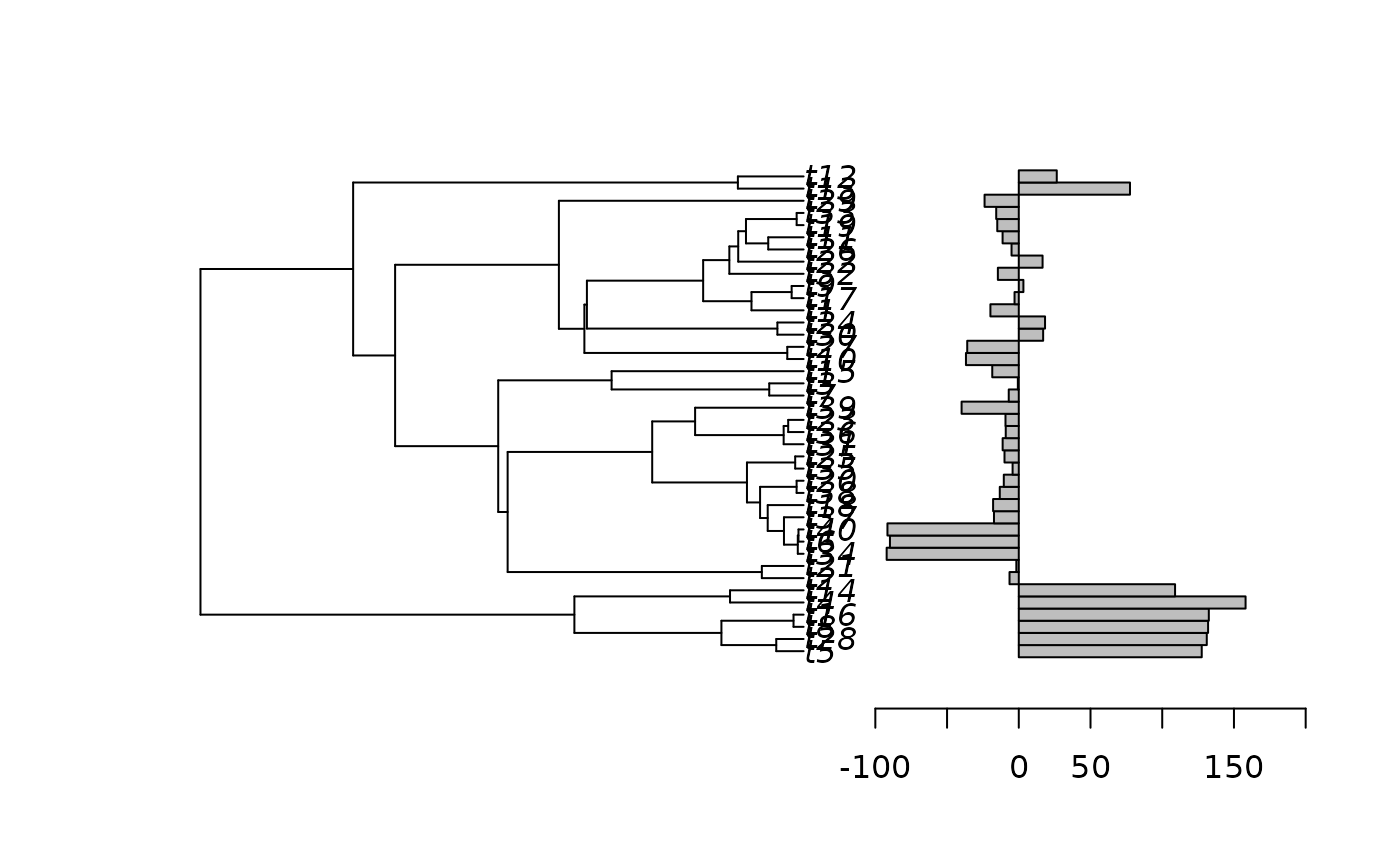# Many trait
y <- rTraitCauchy(n = 10, phy = phy, model = "cauchy",
                  parameters = list(root.value = 0, disp = 0.1))
head(y)
#>            [,1]       [,2]      [,3]        [,4]        [,5]        [,6]
#> t1    -4.059334   10.03650  22.03857  -27.538355 1175.437924 1241.604903
#> t2    37.294124   12.89517  21.47235  -66.985763   21.582613 1238.060210
#> t3    82.599713 -170.83520  44.05055  -57.617606  -59.598502 1213.773019
#> t4   144.714538 -132.53897 310.66940    4.858611    5.046497   24.613782
#> t5 -1813.003405 -128.84778  34.49181   23.309434    2.057757   -6.671051
#> t6    45.697794   95.46919 228.47125 -240.143874  -27.125454 1064.289837
#>         [,7]        [,8]      [,9]      [,10]
#> t1 -37.53598    5.187966  56.31571 -25.531966
#> t2 -24.05523  -95.918020  13.61329  -2.042555
#> t3 -76.77719  -90.300979  43.79448 -26.198105
#> t4 -70.59075  -41.986502 128.55073   2.871317
#> t5 -11.96752 4021.965140 126.51943  49.187235
#> t6  21.74661 -349.044479  61.22999 -11.728113